Graph Hawkes Transformer

Hawkes过程

发布日期: 2023-09-04

[TOC]

这是我首次读到关于 hawkes过程的用transformer实现的，当然后面也是有另外一个新的，那么我就在这里简单介绍一下这篇论文。

首先我们先区分一下几种算法之间的区别

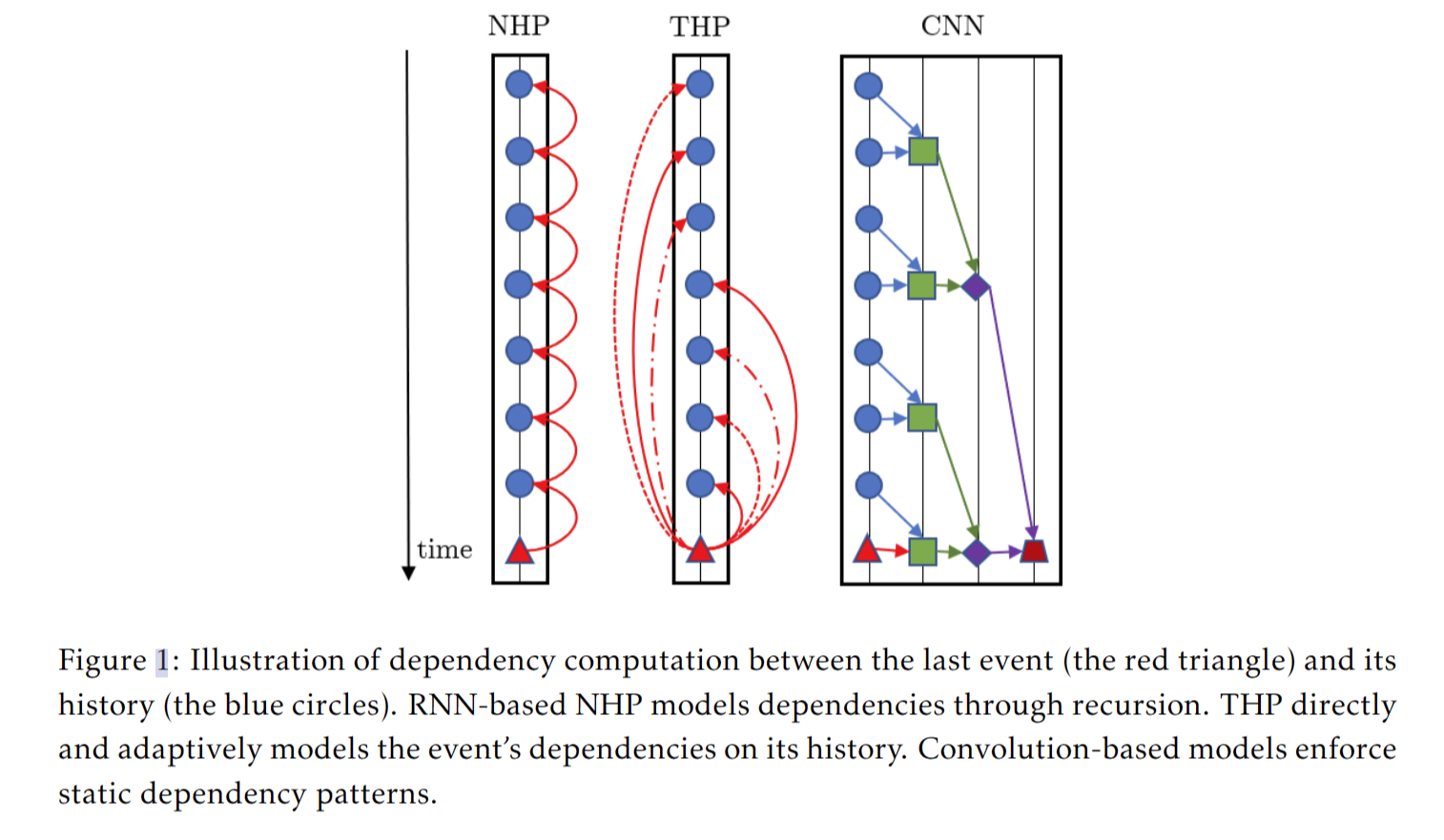
THP 在计算所有事件的依赖关系时允许完全并行，即任意两个事件对之间的计算是相互独立的。这产生了一个表现出强大效率的模型。

将架构推广到连续时间域

在这里我们就不去介绍Hawkes的简单介绍，你可以去前面的文章中去查看Hawkes的具体算法

We introduce our proposed Transformer Hawkes Process. Suppose we are given an event sequence

Transformer Hawkes Process

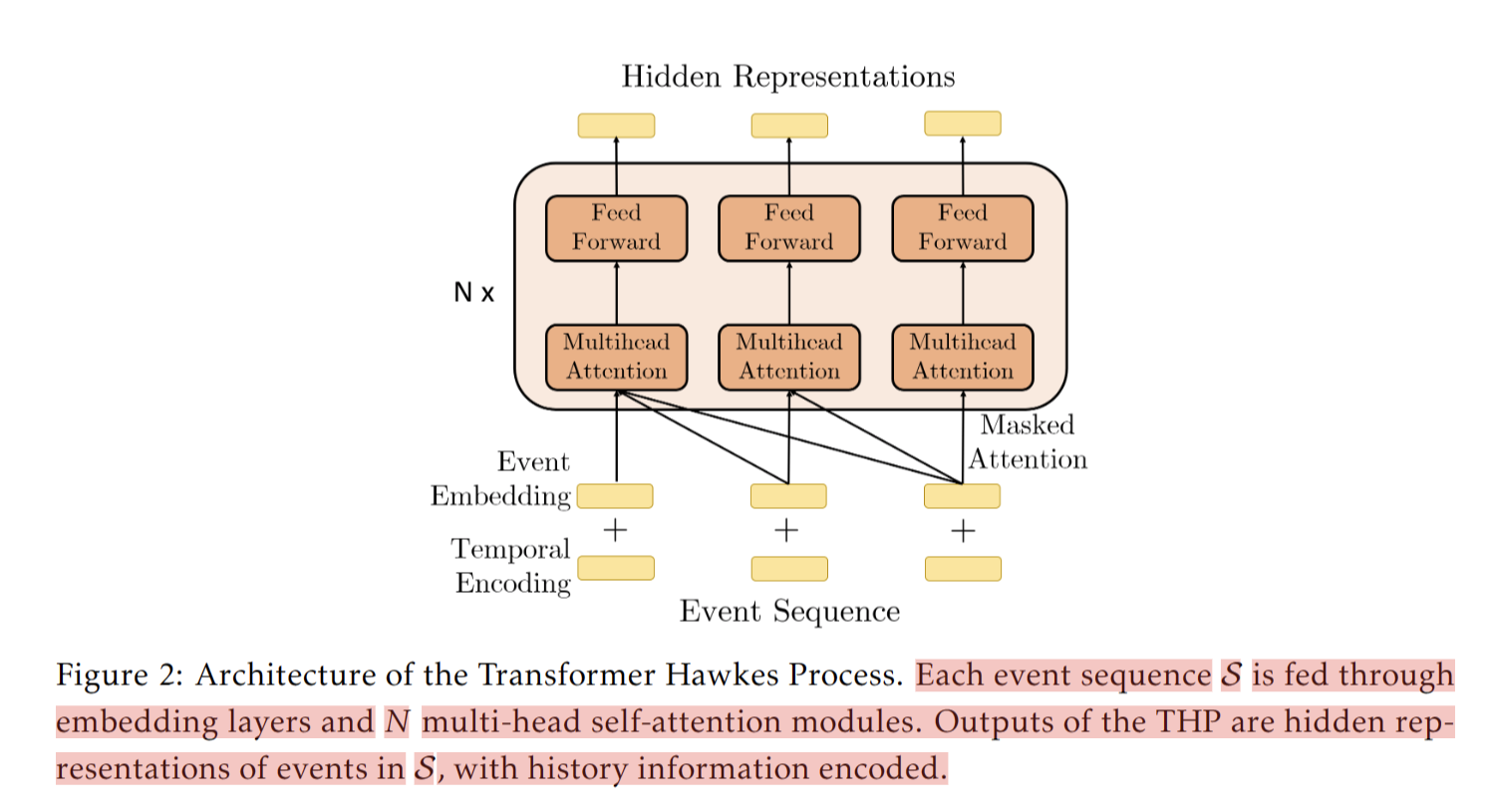
每个事件序列 S 通过嵌入层和 N 个多头自注意力模块馈送。THP 的输出是 S 中事件的隐藏表示，编码历史信息。

下面和transformer里面的相同，都是加入位置编码 M为维度

也存在其他的方法：对于线性序列，边可以捕获有关输入元素之间的相对位置差异的信息。我们考虑的最大相对位置被剪裁为 k 的最大绝对值。我们假设精确的相对位置信息在某些距离之外没有用处。裁剪最大距离也使模型能够泛化到训练期间没有看到的序列长度。（相对位置）

todo：可以考虑怎样去处理创建一个新的属于自己的位置时间编码

我们训练了一个嵌入矩阵U（M×K）对于事件的类型type k，其中 U 的第 k 列是事件类型 k 的 M 维嵌入

kj我们指定为一个one-hot向量，用来指定编号。则每个事件的嵌入就是Ukj

对于每一个事件来说（tj，kj）时间编码 z(t**j) 和事件嵌入Ukj 为RM。然后指定事件序列的嵌入为 Y是事件类型集合的one-hot编码

Z是事件时间编码的集合

X的每一行对应于序列中特定事件的嵌入。

下面通过自注意力模块传递X X 乘以权重缩放进行 softmax 多头的权重不同（可以采用随机配置网络吗？）最后得到聚合结果 output S

然后进入feed forward 前馈网络其中W和b都是神经网络的参数

结果H包含输入序列中所有事件的隐藏表示，其中每一行对应一个特定事件。

Continuous Time Conditional Intensity

时间点过程动力学由连续条件强度函数描述。5 只为离散的时间戳生成隐藏表示，相关强度也是离散的。因此需要一个插值的连续时间强度函数。其中k是指event type Ht是指到目前为止需要考虑的历史的集合

时间定义在区间 t ∈ [tj , tj+1) 上，fk (x) 为softplus 函数。确保强度为正

“current”影响是两个观察到的时间戳 tj 和 tj+1 之间的插值，αk 调节插值的重要性。事实上，除了观察到的事件 {(tj , kj )} 之外，等式 6 在任何地方都是连续的。

“history”由两部分组成：一个向量 wk，它将 THP 模型的隐藏状态转换为标量，隐藏状态 h(t)本身将过去事件编码到时间 t。

“base”强度表示不考虑历史信息的事件出现的概率。

根据上面的强度函数，可以根据此来进行预测也就是求概率，一般的霍克斯过程去进行预测。

自注意力机制里面的差不多

training

对于观察区间 [t1, tL] 上的任何序列 S，给定其条件强度函数 λ(t|Ht )，对数似然为通过最大化所有序列的对数似然来学习模型参数。具体来说，假设我们有 N 个序列 S1、S2、。, SN ，则目标是找到求解的参数优化采用 Adam算法和层归一化 layernorm 和 resnet 残差链接加入进行优化

非事件对数似然

Structured Transformer Hawkes Process

THP 相当通用，可以合并额外的结构知识。我们考虑多个点过程，其中其中任何一个都可以相关。这种关系通常由图 G = (V , E) 描述，其中 V 是顶点集，每个顶点都与一个点过程相关联。此外，E 是边集，其中每条边表示对应两个顶点之间的关系信息。

这不就是三元组

？难道这就是时序知识图谱应用ght的由来？

图编码顶点之间的关系，并进一步表示潜在的交互。建议使用单个 THP 对所有点过程进行建模，顶点点过程的异质性由顶点嵌入方法处理。引入了另外一个坐标，作为顶点，引入嵌入矩阵E作为表示。同理注意力机制的输入也要进行修改。矩阵 A ∈ RL×L 是顶点相似度矩阵，其中每个条目 Aij 表示两个顶点 vi 和 vj 之间的相似度，Ω ∈ RM×M 是要学习的度量。为了将图自注意力模块扩展到多头设置，我们对不同的头使用不同的度量矩阵

可以堆叠多个多头自注意力模块以学习高级表示，这是一种能够学习顶点之间复杂相似性的特征。

此外，顶点相似度矩阵能够对更复杂的结构化数据进行建模，例如动态演化图上的序列。

其中每种类型的事件都有自己的强度，我们为每个事件类型和每个顶点定义了一个不同的强度函数。具体来说，最大化下面的值

这里 Lgraph(V, Ω) 是一个正则化项，当 vj 和 vk 之间存在边时，它鼓励 Vj ΩVk 变大。这意味着如果两个顶点在图 G 中连接，则正则化器将促进它们之间的注意力，反之亦然。请注意，在最简单的情况下，方程式中的 A 可以是邻接矩阵的一些变换，即如果 (vi , vj ) ∈ E，则 Aij = 1，否则为 0。然而，我们认为这个约束过于严格，即一些连接的顶点可能不会表现相似。因此，我们将图视为指导，并引入正则化项，鼓励 A 与邻接矩阵相似，但不强制执行它。这样，我们的模型更加灵活