[TOC]

SAHP 采用 self-attention 来总结历史事件的影响并计算下一个事件的概率。

自注意力适应以增强强度函数的表达能力。该方法增强了模型预测和模型可解释性。

结构图如下

结构图

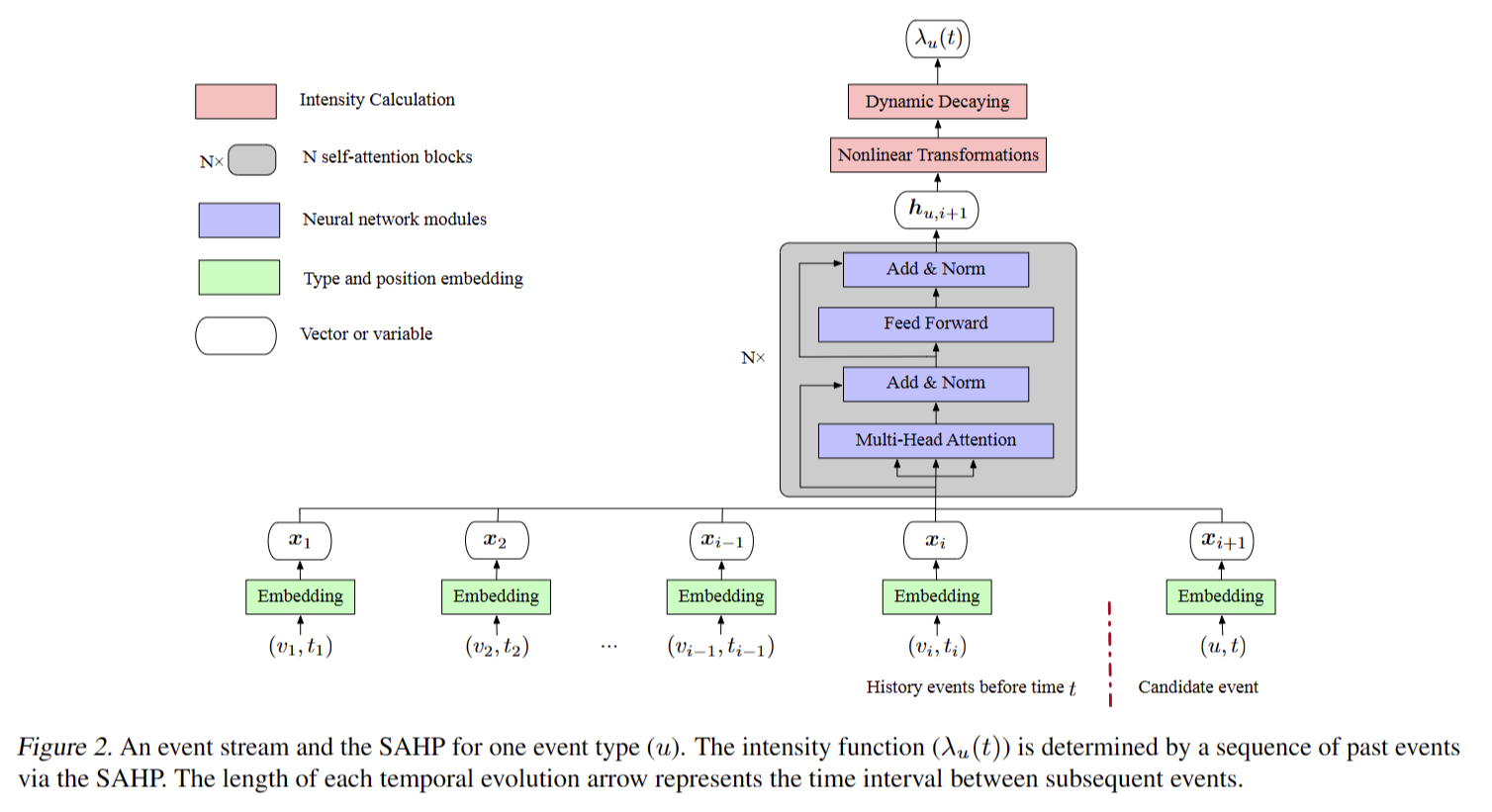
传统的自我注意的一个缺陷是位置嵌入只考虑序列中的序号，忽略了时间事件之间的时间间隔。为了克服这一缺陷，我们通过将时间间隔转换为正弦函数的相移来修改传统方法，因为学习到的注意力权重揭示了一种事件类型对另一种类型发生的贡献。

自注意力导图

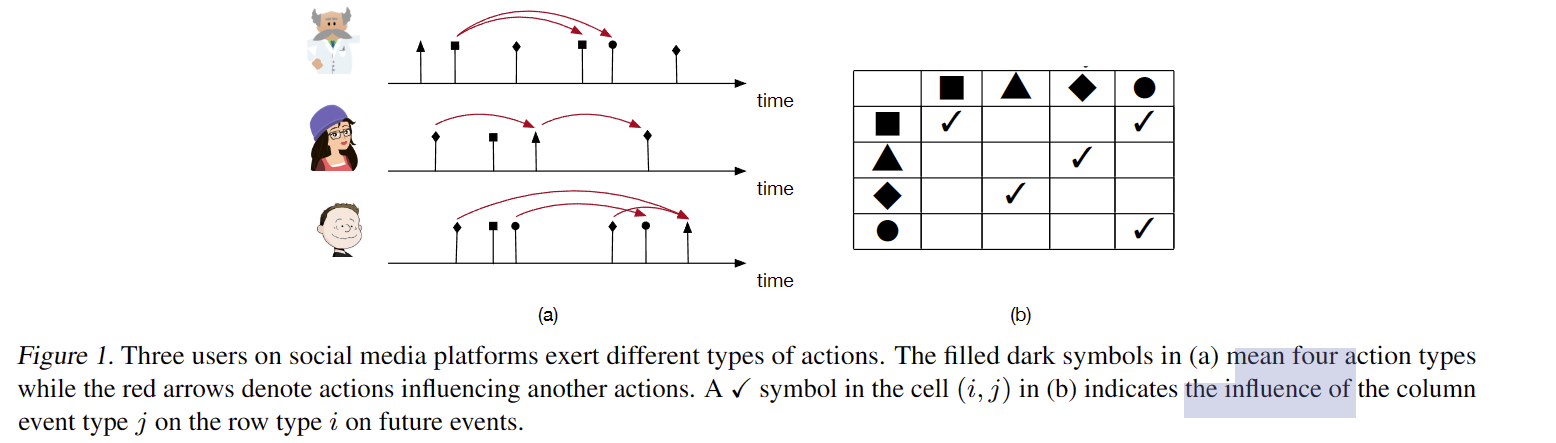
跳跃的影响，也不是跳跃就是超脱了顺序的一个一个的限制

一个是概率的强度函数，一个是累积下来的强度函数

表示过去的每个事件对当前事件的发生都有积极的贡献，这种影响会随着时间的推移而减少。

这个公式的一个主要限制是简化历史事件永远不能抑制未来事件的发生，这在复杂的现实场景中是不现实的

你可以看我的 另外的 文章 图神经Hawkes的过程 可以有关于 强度函数的关系。 其中第一项是过去事件的对数强度函数的总和，第二项对应于无限多个非事件的对数似然。直观地说，无穷小时间间隔 [t, t + dt) 中没有任何类型事件的概率等于 1 − λ(t)dt，其 log 为 −λ(t)dt。

为了应用MLE，基于负对数似然导出损失函数。推导的细节可以在附录中找到。时间间隔[0，T]上的多元Hawkes过程的可能性由下式给出

Self-Attentive Hawkes Process

Event type embedding.

输入序列由事件组成。为了获得每种事件类型的唯一密集嵌入，我们使用线性嵌入层

释：一个 one-hot 向量是指在机器学习和编码中常用的一种表示方法。它是一个二进制向量，其中只有一个元素为1，其余元素都为0。

假设有一个包含n个类别的集合，那么每个类别可以用一个唯一的整数进行编码，从 0 到 n-1。然后，使用 one-hot 编码将这些整数表示为对应的二进制向量。

Time shifted positional encoding.

修改了位置编码，加入了时间要素 k维的向量 其中 i 是序列中事件的绝对位置，ωk 是第 k 维的角度频率，它是预定义的，不会改变。虽然wk是一个缩放参数，它将时间戳ti转换为第k维的相移。多个具有不同ωk和wk的正弦函数用于生成多个位置值，其连接是新的位置编码。pe 的偶数和奇数维度分别从 sin 和 cos 生成。

时间编码

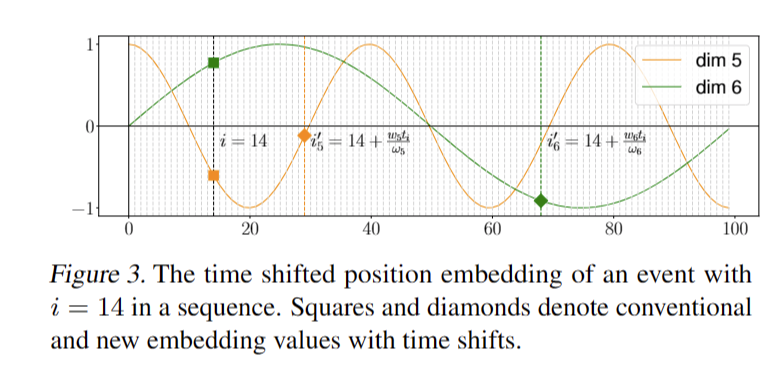
显示了传统和新的位置编码是如何工作的。假设事件 (vi, ti) 位于序列的 i = 14 位。传统方法计算i = 14位置正弦函数的值作为该事件的位置值。我们的编码通过将原始位置 i 移动到一个新的位置来修改这一点，其中 k 表示嵌入维度。这相当于插值时域并产生更短的等长时间段。因此，序列中的位置被时间 ti 移动。时间段的长度由wkωk决定。由于wk和ωk是维度特定的，一个维度的变化可能与其他维度不同。

Historical hidden vector.

相加

Self-Attention.

计算前一个事件对下一个事件的成对影响。这生成一个隐藏向量来总结所有先前事件的影响 在训练期间通过防止模型学习未来事件，向模型提供时间信息。我们通过屏蔽对应于未来事件的输入序列中的所有值来实现注意力机制中的这一点。因此，一个事件的强度仅基于其历史得到。

masked 掩码机制

Intensity function

由于 Hawkes 过程的强度函数依赖于历史，我们通过以下三个非线性变换根据历史隐藏向量计算强度函数的三个参数 函数 gelu 表示非线性激活的高斯误差线性单元。 强化函数定义

强度函数设置的不同。

强度函数设置为下图

预测

预测未来事件

给定历史的信息，求取概率，积分求和

然后是预测下一个时间的时间点发生在什么时候

最后的事件预测可以相等于下面的式子，也就是说我们每一个事件的概率和时间都可以进行预测。