[TOC]
Introduce
Hawkes过程是一种自激励点过程,用于对事件序列建模和分析。它的核心概念包括以下几个要素:
强度函数(Intensity function):强度函数 λ(t) 是Hawkes过程中的关键和核心概念之一。它描述了事件发生的速率或密度,并根据历史事件的发生情况推断未来事件的发生概率。强度函数可以根据时间的变化进行建模,根据历史事件的发生情况对未来事件的发生进行建模,表达事件之间的相互影响。
强度函数通常表示为 λ(t),其中 t 表示时间。它是一个关于时间的非负函数,用于衡量在给定时间 t 下事件发生的强度。强度函数的大小表示相应时间点上事件发生的可能性或密度,即在该时刻触发事件的概率。它决定了事件之间的相互激励关系以及事件发生的模式。通过对强度函数的建模,我们可以探索事件序列中的集群现象、自激励特性以及事件间的传播效应。
基线强度(Baseline intensity):基线强度表示在没有任何事件触发的情况下,事件发生的基础速率。它通常是一个常数或随时间变化的函数,用于描述系统的固有活动水平。
冲击函数(Impulse response function):当某个事件发生时,它可能对后续事件的发生产生影响。冲击函数衡量了这种事件触发的影响程度。通过对冲击函数的建模,可以揭示事件之间的激励传播、相互作用以及可能出现的集群效应。
存在性函数(Existence function):存在性函数表示在给定时间段内事件的存在与否。它与强度函数之间存在一种关系,决定了事件在时间轴上的出现时刻。
这些概念共同构成了Hawkes过程的核心,通过对它们的建模和参数估计,可以分析事件序列中的动态特性、相互影响关系以及事件的发生模式。Hawkes过程在金融、社交网络、地震等领域有广泛应用,可以揭示事件之间的相关性和传播机制,具有重要的研究和实际价值。
为了对相关事件序列进行建模,Hawkes (1971) 提出了一个自激点过程,现在被称为霍克斯过程。Hawkes过程假设过去的事件对未来事件的可能性有激励效应,这种激励随时间呈指数衰减。该模型在某些领域很有用,例如建模地震(Ogata,1998)。
然而,它无法捕获一些真实世界的模式,其中不同类型的过去事件可能对未来的事件有抑制作用,即滑板购买可能会抑制自行车购买。为了解决这个限制,神经 Hawkes 过程 使用具有连续状态空间的循环神经网络概括了 Hawkes 过程,使得过去的事件可以以复杂和现实的方式激发和抑制未来的事件。
然而,神经霍克斯过程只能用少量事件类型对事件序列进行建模,无法准确捕捉大规模时间关系数据中的相互影响。
Graph Hawkes Network (GHN)
我们连续对 tKG 中的离散事件进行建模,我们连续对 tKG 中的离散事件进行建模,分析了以前的问题评估指标,并提出了一种新的时间知识图链接预测排名度量
Hawkes过程是一个随机过程,用于对连续时间中发生的顺序异步离散事件进行建模,其中异步意味着连续事件之间的时间间隔可能不相同
Hawkes 过程假设过去的事件可以暂时激发未来的事件,其特征在于定义如下的强度函数:
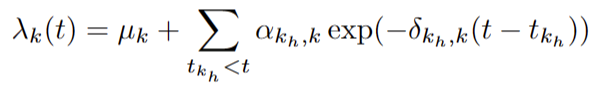
强度函数 λk(t) 表示单位长度区间内类型 k 的预期事件数。
其中μk≥0是事件类型k的时间无关基强度(基线强度(Baseline intensity)
一个是瞬间激发类型强度,也就是冲击函数(当某个事件发生时,它可能对后续事件的发生产生影响。冲击函数衡量了这种事件触发的影响程度。通过对冲击函数的建模,可以揭示事件之间的激励传播、相互作用以及可能出现的集群效应。),一个是激发的衰减率
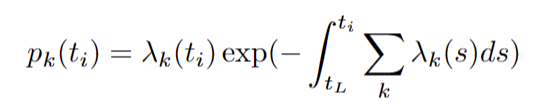
强度函数积分 以及没有事件从tL到ti的概率 其中 tL 表示事件的最新发生时间,而不考虑其事件类型。
Model
受到ReNet的启发,我们进行了相似的工作。
首先是我们给定了一个query(s,r,?,t)我们用来预测实体 o ,
我们用 e来代表嵌入的关系,用i来代表哪一个是谁 ,时间t 不用说
我们定义了一个相关的历史事件序列用于在给定实体预测查询的情况下预测缺失的主题实体(?,r,o,t)
聚合部分
该模块采用 Otj (esi , epi) 中对象实体的嵌入向量的元素均值:
The Graph Hawkes Process
我们将时间建模为随机变量,并在TKGs上部署 Hawkes 过程以捕获底层动态并将其命名为 Graph Hawkes 过程。与具有参数形式的经典 Hawkes 过程相比,我们使用循环神经网络来估计图 Hawkes 过程的强度函数。传统上,循环神经网络用于将序列与均匀间隔的间隔同步。
我们使用具有显式时间依赖性隐藏状态的连续时间 LSTM,其中隐藏状态在每次事件发生时立即更新,并且还随着两个相邻事件之间的时间间隔而不断演变。
根据我们的意图 我们构建 相应的强度函数
h(eo, esi , epi , ti, eh,sp i ) (里面的元素可以为正负)∈ Rd (d 表示隐藏维度的数量) 表示连续时间循环神经网络的隐藏状态,它以 eh,sp i 作为输入并总结相关历史事件序列中的信息,⊕ 表示连接算子。
我们将主题实体嵌入和谓词嵌入与隐藏状态向量连接起来,让模型从主谓对中捕获重要信息,因为它是我们可以从对象预测查询 (esi , epi ,., ti)。
Wλ ∈ R(2r+d)×r 是线性层的权重矩阵,用于将连接的维度从 2r + d 转换为 r,以便我们可以在它与对象候选 eo 的嵌入之间进行点积,以便网络可以捕获主题 esi 和对象候选 eo 的兼容性,考虑它们的先前交互。
这解释了实体倾向于与其他具有相似近期行动和目标的实体形成关系的行为
当事件发生时,强度向量 λ的所有元素都应该在所有时间戳上严格为正。因此我们需要一个激活函数 f (x),以便强度向量的每个元素可以满足我们的要求。
那么就是softplus 函数
LSTM

在时间戳 tm 中,我们将输入 km 输入到网络中并更新门函数和内存单元。
为了捕获历史事件序列中的累积知识,输入 km 将基于 Otm (esi , epi ) 的邻域聚合与相应的主题实体 esi 和谓词 epi 的嵌入向量连接起来作为连续时间 LSTM 的输入。
对每个状态和门函数进行离散更新
更新不依赖于最后一次更新 h(tm-1) 的隐藏状态,而是依赖于时间戳 tm 处的值 h(tm)。
等式25使得单元函数 c(t) 在 LSTM 的每个更新处瞬间跳转到初始单元状态 cm+1,然后不断向目标单元状态 -cm+1 漂移,这反过来控制隐藏状态向量和强度函数。
因此,在两个更新时间戳(tm, tm+1]之间,c(t)遵循指数曲线来处理目标单元状态。
等式 26 描述了 c(t) 如何在离散时间 LSTM 模型中控制类似于 hm
的隐藏状态向量 h(eo, esi , epi , t,
eh,sp),该模型从过去的事件序列中提取相关信息
因此,这种循环架构能够使用历史信息对给定时间知识图的复杂非线性和演化动力学进行建模。
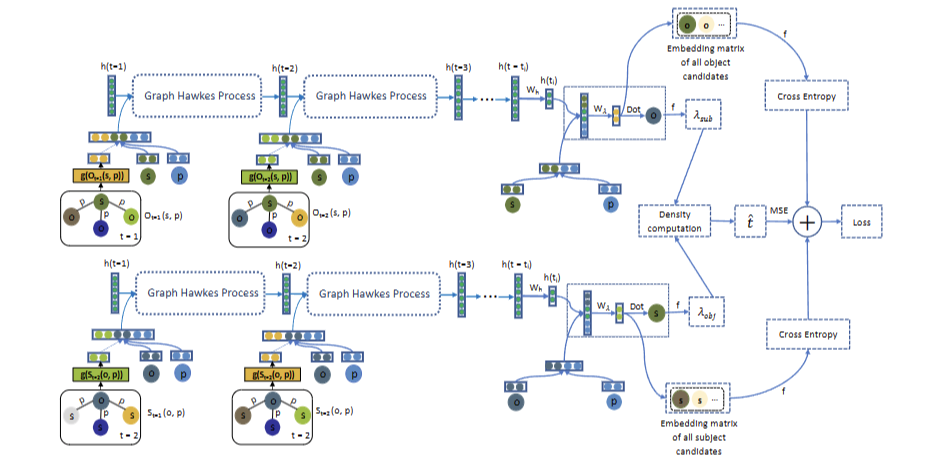
图霍克斯网络架构的可视化。在这里,我们专注于一个特定的训练四元组 (esi , epi , eoi , ti),其中 esi , epi 和 eoi 的嵌入分别表示为绿色节点、蓝色节点和青色节点。h(t) 代表 cLSTM 中的隐藏向量。f是缩放的软加函数,其中 f (x) = ψ log(1 + exp(x/ψ))。Graph Hawkes Network 使用邻域聚合和图 Hawkes 过程来总结 Ot 中主题实体 esi 和对象实体之间的交互,以及对象实体 eoi 与 St 中不同时间戳的主题实体之间的交互,并推导出四元组的强度函数预测任务。
链接预测
tL是指最近的时间戳
因此,我们可以直接比较它们的强度函数 λ(eo|esi , epi , ti, eh,sp i ),以避免计算成本高的积分计算。然后,我们按照这个密度的降序对所有候选者进行排序,以对对象位置的正确实体进行排名。 即出现的概率最大化
时间预测
对于时间预测任务,给定一个事件 (esi , epi , eoi
),我们的目标是根据观察到的事件预测其下一个发生时间的期望值。由于我们对涉及的主题实体和对象实体有完整的信息,我们可以利用
eh,sp i 和 eh,op i。因此,未来时间发生事件类型 (esi , epi , eoi )
的强度定义如下:
参数学习
由于链接预测可以看作是一个多类分类任务,其中每个类对应一个实体候选,我们使用交叉熵损失来学习链接预测:
我们通过使用超参数 w 缩放前者来平衡时间预测任务的损失和链接预测任务的损失。
伪代码



